Solving schedule collisions with geometric algorithms
Introduction
Imagine you're given 100,000 points scattered across a plane. Your task seems simple: find the closest pair of points. The naive approach would compare every possible pair, resulting in nearly 5 billion comparisons. But what if I told you there's a technique that could solve this in almost linear time?
This elegant approach—the line sweep algorithm—turned out to be the solution to a seemingly unrelated problem I encountered years later. Let me share how this geometric algorithm became the unexpected hero in my event scheduling system.
This elegant approach—the line sweep algorithm—turned out to be the solution to a seemingly unrelated problem I encountered years later. Let me share how this geometric algorithm became the unexpected hero in my event scheduling system.
How I Discovered Line Sweep: A Scheduling Analysis Dilemma
The problem was deceptively simple: find all overlapping time slots across thousands of appointments in our scheduling system. My first instinct was the brute-force route—compare every pair of slots and check for collisions. Whether done in SQL or in memory, the approach quickly crumbled under real-world scale. With thousands of slots being logged daily across multiple time zones, the computation became unmanageable.
I wasn't willing to settle for batching, it felt like conceding defeat. That's when a distant memory resurfaced: the line sweep.
If you imagine every appointment as a start and end point on a 1D timeline, the collision problem transforms into something strikingly geometric. By "sweeping" through the sorted list of start and end times, you can track how many appointments are active at any moment—and spot overlaps efficiently.
What once felt like a messy data problem suddenly had a clean, elegant algorithmic core. The line sweep turned out to be the key, transforming our slow and clunky analytics into something snappy.
I wasn't willing to settle for batching, it felt like conceding defeat. That's when a distant memory resurfaced: the line sweep.
If you imagine every appointment as a start and end point on a 1D timeline, the collision problem transforms into something strikingly geometric. By "sweeping" through the sorted list of start and end times, you can track how many appointments are active at any moment—and spot overlaps efficiently.
What once felt like a messy data problem suddenly had a clean, elegant algorithmic core. The line sweep turned out to be the key, transforming our slow and clunky analytics into something snappy.
Understanding Line Sweep
At its core, the line sweep algorithm works by imagining an invisible line (usually vertical) that sweeps across the plane from left to right, stopping at important points. Rather than considering all geometric objects simultaneously, we only focus on the objects that intersect with our sweeping line at any given moment.
Think of it like scanning a room with a laser beam—instead of trying to process everything at once, you examine only what the beam illuminates as it moves across the space. This approach dramatically reduces the computational complexity.
The key components of any line sweep algorithm include:
Think of it like scanning a room with a laser beam—instead of trying to process everything at once, you examine only what the beam illuminates as it moves across the space. This approach dramatically reduces the computational complexity.

The key components of any line sweep algorithm include:
- The Sweep Line: A conceptual line that moves across the plane
- Events: Points where we need to update our data structures (like when the sweep line hits a new point)
- Status Structure: A data structure that maintains information about objects currently intersecting the sweep line
Solving the Closest Pair Problem
Let's apply the line sweep technique to find the closest pair of points among n points in a plane—a problem that would normally require O(n²) comparisons.
The algorithm works as follows:
As we process each point p:
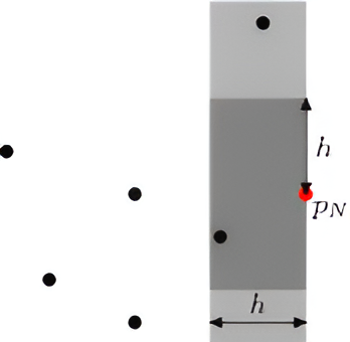
The brilliance of this approach is that we don't need to compare every pair of points. At each step, we only consider points within a narrow vertical strip of width 2δ around our current point. And within this strip, we only look at points within a distance δ above or below our current point.
A key insight: within any strip of width δ, there can be at most a constant number of points that are at least δ apart from each other. This means each point is compared with only a constant number of other points, resulting in an O(n log n) algorithm overall.
The algorithm works as follows:
- Sort all points by their x-coordinates (taking O(n log n) time)
- Initialize a variable δ to track the minimum distance found so far (set to infinity initially)
- Create an empty balanced binary search tree (BST) to store points sorted by their y-coordinates
- Sweep a vertical line from left to right, processing each point
As we process each point p:
- Remove all points from our BST that have x-coordinates less than (p.x - δ), as they cannot form the closest pair with p
- Search the BST for all points with y-coordinates between (p.y - δ) and (p.y + δ), as only these points could potentially be closer than our current minimum
- Calculate the distance between p and each potential candidate, updating δ if we find a smaller distance
- Insert p into the BST

The brilliance of this approach is that we don't need to compare every pair of points. At each step, we only consider points within a narrow vertical strip of width 2δ around our current point. And within this strip, we only look at points within a distance δ above or below our current point.
A key insight: within any strip of width δ, there can be at most a constant number of points that are at least δ apart from each other. This means each point is compared with only a constant number of other points, resulting in an O(n log n) algorithm overall.
Translating Line Sweep to Time: Solving the Collision Problem
The breakthrough moment came when I realized that time intervals could be treated just like geometric objects. An event with start and end times is conceptually similar to a line segment with start and end points. The collision detection problem in my scheduling system was fundamentally a line segment intersection problem—just along a one-dimensional timeline rather than in 2D space.
Here's how I implemented the solution:
1. Transform events into time points: Each event generates two time points—a start point (adding 1 to our "active count") and an end point (subtracting 1)
2. Sort these time points chronologically: This is our "sweep line" moving through time
3. Detect collisions: Wherever the active count exceeds 1, we have overlapping events
The beauty of this solution is its efficiency. Instead of comparing every possible pair of appointments (n²), we process just 2n time points (start and end for each appointment) in sorted order. The time complexity drops to O(n log n), again dominated by the sorting step.
Here's how I implemented the solution:
1. Transform events into time points: Each event generates two time points—a start point (adding 1 to our "active count") and an end point (subtracting 1)
-- Start points (value = 1)
SELECT start_time AS time_point, 1 AS event_value, id, user_id
FROM appointments
WHERE date = '2025-05-18'
UNION ALL
-- End points (value = -1)
SELECT end_time AS time_point, -1 AS event_value, id, user_id
FROM appointments
WHERE date = '2025-05-18'
2. Sort these time points chronologically: This is our "sweep line" moving through time
SELECT
time_point,
id,
user_id,
event_value,
-- Running sum tracks active events at each moment
SUM(event_value) OVER (ORDER BY time_point) AS active_count
FROM sweep_events
ORDER BY time_point
3. Detect collisions: Wherever the active count exceeds 1, we have overlapping events
-- Finding user-specific conflicts
SELECT
s1.id AS slot1_id,
s2.id AS slot2_id,
s1.user_id,
s1.time_point AS collision_point
FROM sweep_state s1
JOIN sweep_state s2 ON
s1.time_point = s2.time_point AND
s1.id < s2.id AND
s1.user_id = s2.user_id AND
s1.event_value = 1
WHERE
s1.active_count > 1
The beauty of this solution is its efficiency. Instead of comparing every possible pair of appointments (n²), we process just 2n time points (start and end for each appointment) in sorted order. The time complexity drops to O(n log n), again dominated by the sorting step.
Beyond Basic Collision Detection
Once I had the foundation in place, I could extend the solution to handle more complex business rules:
By adding a few additional dimensions to our sweep, we could answer complex questions that would have been computationally expensive with traditional approaches.
- User-specific conflicts: Finding cases where the same person is double-booked
- Room-specific conflicts: Identifying overlapping bookings for the same physical space
- Resource utilization: Determining peak times when we need additional staff
- Capacity planning: Visualizing time periods with the highest booking density
By adding a few additional dimensions to our sweep, we could answer complex questions that would have been computationally expensive with traditional approaches.
The Elegant Transformation
What fascinates me most about this algorithm is how elegantly it transforms dimensions. In the closest pair problem, it reduces a two-dimensional search space to a manageable one-dimensional sweep. In my scheduling problem, it transformed a complex temporal relationship question into a simple counting exercise along a timeline.
This dimensional reduction is what gives the line sweep algorithm its power across seemingly unrelated domains. Whether you're working with points in a plane or events in time, the core principle remains the same: sweep through one dimension in order, maintaining only the information needed at each step.
Sometimes great solutions come from unexpected places—in my case, from a computational geometry algorithm I'd studied years earlier. It's a reminder that algorithmic thinking transcends specific domains, and elegant solutions often have surprising applications.
This dimensional reduction is what gives the line sweep algorithm its power across seemingly unrelated domains. Whether you're working with points in a plane or events in time, the core principle remains the same: sweep through one dimension in order, maintaining only the information needed at each step.
Sometimes great solutions come from unexpected places—in my case, from a computational geometry algorithm I'd studied years earlier. It's a reminder that algorithmic thinking transcends specific domains, and elegant solutions often have surprising applications.